Aufgaben zur Addition und Subtraktion
- 1
Addiere die Vektoren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Addiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Addiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Addiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Addiere die Vektoren komponentenweise.
Da der erste Vektor das negative des zweiten Vektors ist, addieren sie sich zum Nullvektor.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Addiere zuerst die Vektoren in den Klammern komponentenweise.
Addiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
- 2
Subtrahiere die Vektoren.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Subtrahiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Subtrahiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Subtrahiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Subtrahiere die Vektoren komponentenweise in der Klammer.
Subtrahiere die Vektoren komponentenweise.
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren subtrahieren
Subtrahiere die Vektoren komponentenweise.
Vereinfache und subtrahiere die Vektoren wieder komponentenweise.
Hast du eine Frage oder Feedback?
- 3
Addiere die Vektoren:
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Um die beiden Vektoren zu addieren, addierst du einfach ihre Koordinaten.
Zusatz: Skizze der Vektoren
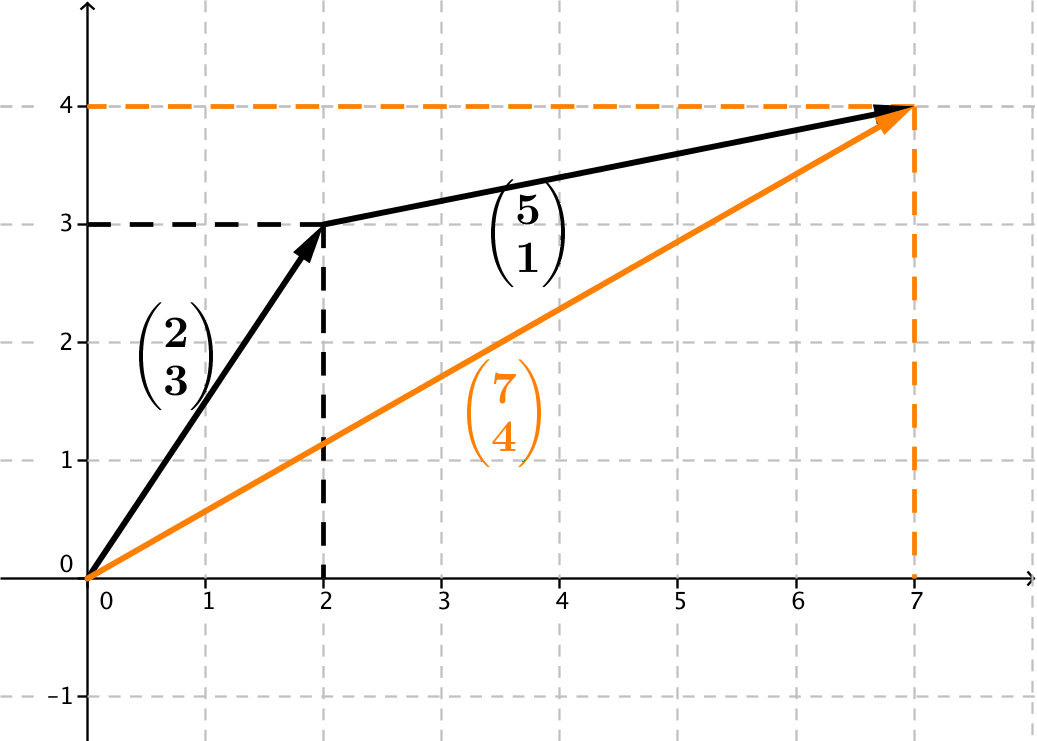
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Um die beiden Vektoren zu addieren, addierst du einfach ihre Koordinaten.
Zusatz: Skizze der Vektoren
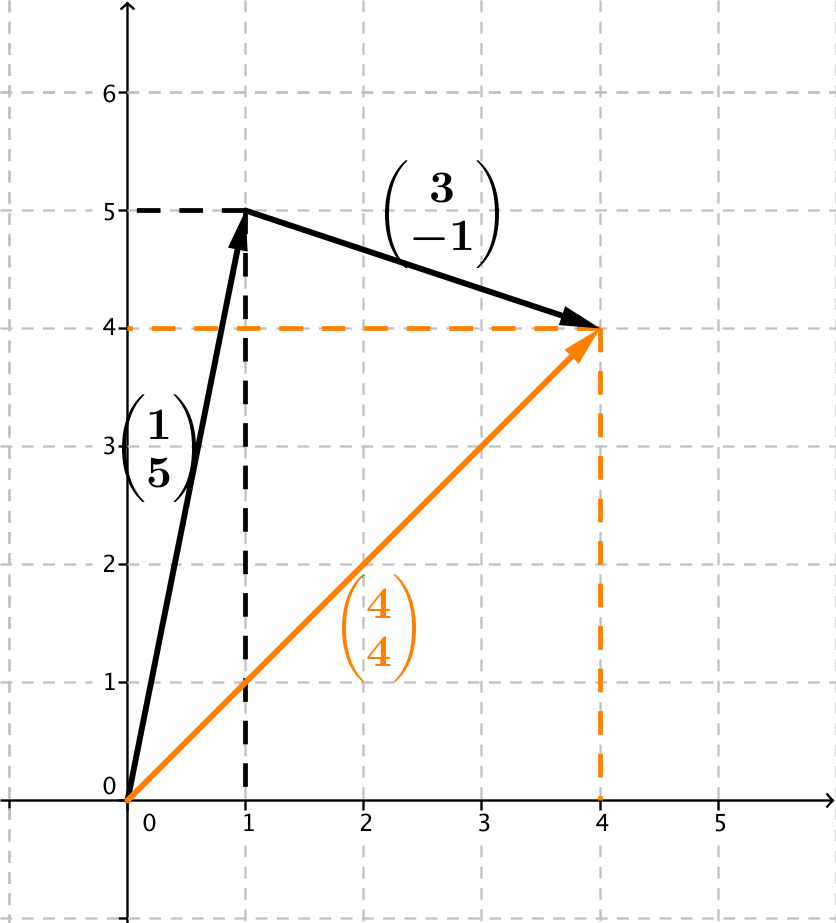
Hast du eine Frage oder Feedback?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Vektoren addieren
Um die drei Vektoren zu addieren, addierst du einfach ihre Koordinaten.
Zusatz: Skizze der Vektoren
Hast du eine Frage oder Feedback?
- 4
Bestimme jeweils das Skalarprodukt der folgenden Vektoren:
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Skalarprodukt wird allgemein gebildet durch
Hier also:
Das heißt: Das Skalarprodukt von und ist .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Skalarprodukt wird allgemein gebildet durch
Hier also:
Hier stehen die Vektoren senkrecht aufeinander, da das Skalarprodukt ist.
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Skalarprodukt wird allgemein gebildet durch
Hier also:
Das Skalarprodukt von und ist .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Das Skalarprodukt wird allgemein gebildet durch
Hier also:
Das Skalarprodukt von und ist . Die Vektoren stehen somit senkrecht aufeinander.
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Benutze die Formel zur Berechnung des Skalarprodukts:
Das Skalarprodukt von und ist . (Die Vektoren stehen also senkrecht aufeinander.)
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Benutze die Formel zur Berechnung des Skalarprodukts.
Das Skalarprodukt von und ist .
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Tipp: Wenn du ganz genau hinschaust, musst du eigentlich nicht rechnen. An welcher Stelle kommt eine Null bei vor? Und an welcher Stelle bei ?
Skalarprodukt berechnen
Das Skalarprodukt zweier Vektoren kannst du anhand der Formel berechnen, wie du hier siehst. Oder du verwendest den Tipp und siehst die Antwort sofort.
Das Skalarprodukt von und ist . (Die beiden Vektoren stehen also senkrecht aufeinander.)
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Skalarprodukt
Tipp: Hier hast du es mit Polarkoordinaten zu tun.
Skalarprodukt berechnen
In dieser Aufgabe kannst du nicht sofort das Skalarprodukt berechnen, da du es mit Polarkoordinaten zu tuen hast, wie der Tipp bereits erwähnt. Deshalb musst du zuerst die Polarkoordinaten in kartesiche Koordinaten umrechnen und anschließend das Skalarprodukt berechnen.
Umrechnung in kartesische Koordinaten
Allgemein gilt für die Umrechnung eines Vektors in Polarkoordinaten :
und
Setze in diese Formel ein.
:
und
: und
Damit erhältst du die folgenden Vektoren in kartesischer Form.
und
Skalarprodukt berechnen:
Das Skalarprodukt wird allgemein gebildet durch
.
Hier also:
Das Skalarprodukt von und ist somit .
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

